Anchor point
-
@DGames135 I love trigonometry, calculus and algebra. In fact, I’m better at that stuff than I am at simple maths 😐
-
@DGames135 its simple....they work great for my projects, so love is what they get! @Aidan-Oxley so since you love trigonometry, do happen to know the math behind rotating on an anchor? Because I don’t LOL
maybe we should start a new thread and get everyone’s opinion on sine and cosine!🤣🤣🤣
-
@iTap-Development if you really want a trig way it shouldn't be too hard, but here's an easy way using move anchors (if I understand what you want): http://bit.ly/2fS4jj8
It moves to the anchor you want to rotate about, rotates, then reverses the movement of the anchor. -
@Jack8680 thanks I check it out....I did want to do a trig way but I can’t figure it out....
-
@iTap-Development I’m trying to make a trig version, but it’s too late for me brain not working past 11 pm lol. It’s gonna end up with like 10x more behaviours than Jack’s version 😝. I’ll do it tomorrow.
-
@Jack8680 I never thought of doing it that way! Thanks!
@Aidan-Oxley lol ok. -
@iTap-Development [0_1507239850952_rotate.tap](Uploading 100%) Here’s a trig version lol. Aww I don’t have the privileges to upload the actual file lol. Link: http://bit.ly/2yrzlps
-
@Aidan-Oxley great I’ll check it out tomorrow....because it’s 9:00 pm here and I’m tired!
-
@Aidan-Oxley hey could you explain the “initial angle” box container and how you’re using it?
-
@iTap-Development It’s the angle from the anchor to the object when the object is at rotation 0°. For example, anchor is 1 metre up and 1 metre to the right (so both positive), so when the object is at 0° rotation, the angle from the anchor to the object is 225° (so that’s down-left). Hope this makes sense.
-
@Aidan-Oxley hey, so I’m just coming back to this(I got a 3d printer so I’ve been busy with that!);
What do you need the “initial angle” for?
And I’m not sure as to the purpose of the behaviors in the screen shot.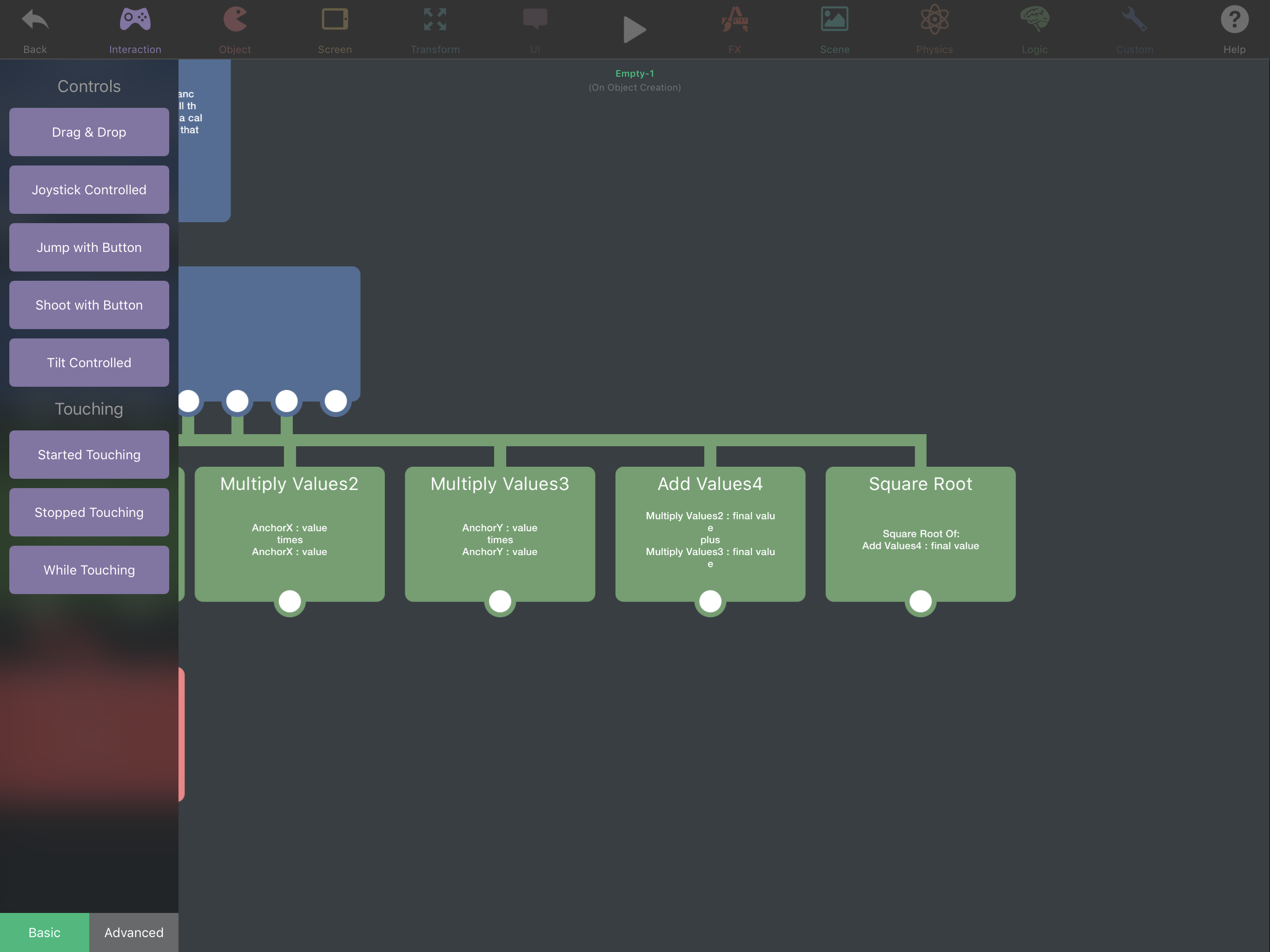
-
@iTap-Development those behaviours are Pythagoras' theorem. The result from the square root is the distance from the centre to the anchor point.
-
@iTap-Development Jack is right. This is how you work out the diagonal distance between two points if you know their coordinates.
-
@iTap-Development A hacky, tacky way to achieve the goal:
Create a dummy object that you'll use as a virtual anchor point. Use the physics weld joint to bind your rotating object to the dummy object at the position you want relative to the virtual anchor point. Then rotate the dummy object. This should give you the result you want, but will ruin anything else regarding physics.
But I agree. The anchor point should be respected by the rotate behaviour.
-
@Deeeds that would work kinda, but yeah it wouldn’t work well in some ways.
-
@Aidan-Oxley @Jack8680 oh duh! So you are just multiplying the x and y by them selves for the x and y distance to the other point?
I think I always just added the actual x and y distances. -
@iTap-Development You know Pythagora’s theorem? If you have a right angle triangle, a is the length of one side, b is the length of the other and c is the length of the hypotenuse (the longest one, diagonal if a is x and b is y), then c² = a² + b². What I was trying to work out is the diagonal distance between two points. I can easily get the x and y distance between them, but I wanted diagonal.
-
@Aidan-Oxley sorry! I was confusing with something else in my project 🤦♂️ I’ve only got a few hours of sleep every night for a week due to my 3d printer addiction! so my brain doesn’t work....
-
@Aidan-Oxley so why are you multiplying the sine and cosine angles by the diagonal distance?
-
@iTap-Development I don’t remember lol. There is a reason though. It’s probably one of those formulas like hypotenuse = sin(θ) × opposite.